Calculus

Derivatives made easy 3a) Maximum and minimum explained

Hi,
in school we learn how to derive right now. The teacher does not do very good job. The class does not know about limits and they only learned power rule and no other rule for derivation though at the same time they learn about maxima and minima.[0]

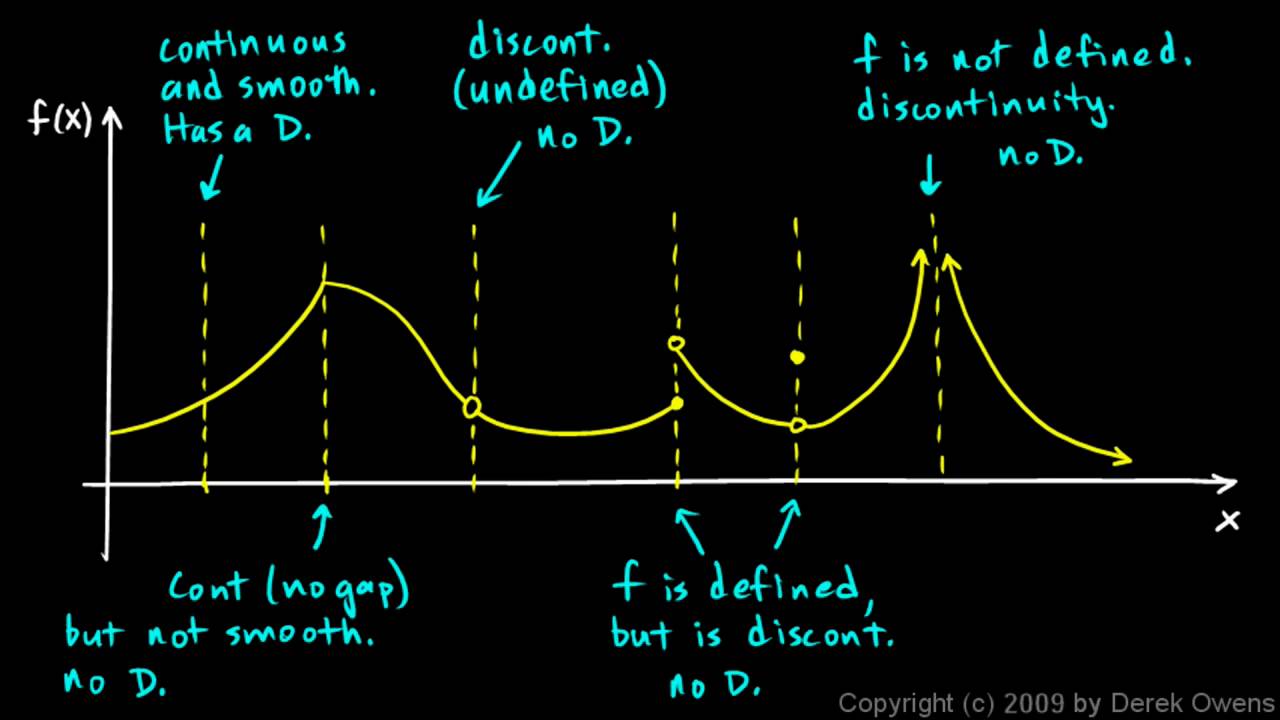
When you derive function you can find lot of useful informations about it. Today I will talk about minima and maxima. Those are points where the function turns around creates “hill” or “valley” – maxima or minima.

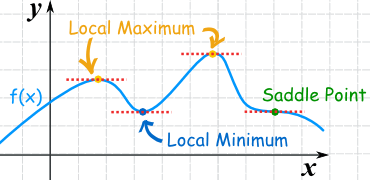
https://www.mathsisfun.com/calculus/images/function-min-max.gif

Some fictional function.

In the function above (f-blue line) you can see couple of points marked. Two orange points are maxima, blue is minima and green is special to which I will get in another post.

 

As I have already said quite few times, when you derive function you will find out what is the slope (how much up or down) at one point[3]. If it does not go up or down it is zero, those are the maxima and minima you are looking for. Right before maximum you have positive slope, the function goes up towards maximum. Right after maximum you have negative slope. What is between if the function is smooth? Zero. When we derive function, lets say function like this:

f(x)=2x²    We get (according to power rule, if you do not know it ignore it right now):

f'(x)=4x    The apostrophe means that it has been derived.

Now when does this derivation equals zero? In other words? When is the slope zero?

Only when x=0 because f'(0)=4*0 = 0 [2]

The original function has minimum or maximum on the point when x=0 [1]. Tricky is that you do not know if it is minimum or maximum which needs some more work and I will get to it in another post.

Dragallur

[0]I will also talk about power rule, multiplication rule and so on in the future.

[1]To get the coordinates of the maximum or minimum you just plug the solution of the derivative to original function and you will get the y coordinate.

[2]If you work with higher order polynomials like x³ you might easily get more solutions which means more minimas and maximas.

[3]If you plot the derivation you will get the slope anywhere.

PS: sometimes I see minima or minimum and maxima or maximum so I use both as I want.

Jerks are even in physics

Hi,
the title is a pun. There are probably jerks yes, but what I want to talk about is physical unit[1] called jerk, it is named like this because jerk not only means, idiot or stupid, but also to move suddenly, because of surprise.

It will be nice, if we first recall that derivation describes the rate of change of something. For example, speed is the first derivative of position because speed describes the rate of change of position, the higher the speed the more position changes!

{\boldsymbol {v}}=\lim _{{\Delta t}\to 0}{\frac {\Delta {\boldsymbol {x}}}{\Delta t}}={\frac {d{\boldsymbol {x}}}{d{\mathit {t}}}}.

1st derivation of position “compared” to time

In the picture above you can see how speed is defined compared to position (x) and time (t). It is its derivative as I said before. Now of course you can define something, that describes how velocity changes over time. That is called acceleration.

\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}

Again, “d” simply means derivation and when it is “squared” it means that you need to derive it twice. Acceleration describes, how velocity changes over time.

This is all you might need for daily life. Of course though, scientists defined next derivations, the change of acceleration in time is called jerk. The change of jerk is called jounce the change of jounce is crackle, next follows pop and then possibly lock, drop, shot and put. The SI units of all of these time, position related things are similar. With each derivation you add one to exponent of time.

v=m/s¹
a=m/s²
j=m/s³

and so on..

Just to remind you, if you have lets say “pop”, which is 6th derivation, of 10 m/s^6 you will have a tremendous speed extremely fast. From this next equation it should be pretty clear:

{\displaystyle {\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}\,t+{\frac {1}{2}}{\vec {a}}_{0}\,t^{2}+{\frac {1}{6}}{\vec {\jmath }}_{0}\,t^{3}+{\frac {1}{24}}{\vec {s}}_{0}\,t^{4}+{\frac {1}{120}}{\vec {c}}_{0}\,t^{5}+{\frac {1}{720}}{\vec {p}}\,t^{6}}

The power of the higher derivations is that the exponent does extreme changes in a moment. r is the position, v speed, a acceleration… p is pop and t is time.

This is probably not used much, if at all, even in engineering.. but hey, fun!

Dragallur

[1]It is not a unit. It is physical quantity or something like that. I do not really know how it is called in english.

Derivatives made easy 2) Non-differentiable functions

Hi,
so I continue with this tutorial. Today I will cover when function is not differentiable. If you want to read the basics check out the last post, it links to limits and continuity which will be important today.

Just to remind ourselves here is the formula that I explained last time:

Basics

It uses limit so logically if the point we are trying to derive is not continous, which means that the limit does not exist there we can not derive. This is not the only thing that can happen to us. Sometimes function is completely continous but from negative side it grows exponentially and from positive side it is linear. Check out the nice picture below:

Continuity

From the whole picture the most important point is the second one. It says: “continous (no gap) but not smooth, not differentiable”. To find this out algebraically you need to know the equations of both left and right part of the function.[1]

If you know them you will insert it into the derivation equation that we used last time as f(x). You have to add h of course as it is the difference between your two points. If both of your solutions equal (right and left side) you know that the function IS differentiable.

Dragallur

PS: ask me if you want to expand any part of the post. I have no problem whatsoever with it and it will make me even happy to write some extra parts.

[1]Yes function can be made up of different parts only on intervals. You can even write something like (odd Xs are equal to 2).

Derivatives made easy 1) Slope on curve

Hi,
today I am going to explain one fundamental equation that is used to calculate derivatives.

Derivative of a function basically says what is the rate of change or the slope of that function. You can have both rate of change of whole function which gives you another function or just at one point which equals to some number. The fundamental thing is to find the slope. Last time I explained this only for a line, not curve. On line the slope is constant but not on curve.

Tangent and secant line.

On the gif above you can see a function. There is a black point that is on the same place. Blue point is getting closer and closer with each step. All the time the black line creates secant line to the curve, it cuts it on two points. When it is red it is tangent line which means that it does not cuts it at all. It is the only one step in which it is just touching. To get the rate of change of curve you need to find this tangent line. Lets call the distance between the two points “h”. The tangent line will exist when h approaches zero.

THE equation. Sometimes f'(x) is written on the left.

This thing above is the equation that we will get when we take coordinates of both points.

black point(  x;f(x)   )                    [1]
blue point  (  x+h;f(x+h)  )           [1]

Just to clear things out, the first thing in the brackets is the x coordinate and the second y coordinate. As I said blue point is moved to side by the distance h and as the distance approaches 0 we are getting tangent line of curve. In the last post I showed that you need to only divide the difference of y coordinates by difference of x coordinates. Check it out if you do not know what I mean.

We will do exactly it to get right part of the equation above without the limit. Only h will be left in the denominator because there is the difference in x coordinates which means:

x+h-x=h

Now to get the tangent line we only add the limit and we have got the fundamental equation of derivates. This we can use for any curve or line that we want to derive. The left part is just a notation for derivation.

Dragallur

PS: be sure to check out this page that lets you interactively create secant and tangent lines.

[1]Just in case you do not understand why there is f(), it is basicly the same as y though we are in functions so we use this kind of notation and yes, f(x)=y. We just add h to get the y coordinate of blue point.

 

Limits made easy and slope

Hi,
today I am going to explain to you very basic concept called the slope. This is going to be important for the basic understanding of derivation.

Slope describes how much is line steep and if it is decreasing, horizontal or vertical. There is simple equation for it.

m=\frac{y_2-y_1}{x_2-x_1}.

m is the slope of a line

m = \tan (\theta)\!

This equation equals the first one because trigonometry

So to get the slope of line at given point you simply pick one point on it which has two coordinates: x1 y1. Then you pick another point to the right side and it is going to have coordinates x2 y2.

Here you can see why tan(theta) is equal to m

The subtraction creates this kind of triangle from which you can either calculate the angle or the m value which is the steepness.

Lets make an example (from wikipedia), lets say we haw line that runs through two points: A=(1,2) B=(13,8)

When we have such a information we can calculate the slope because:

x1=1
y1=2
x2=13
y2=8

All parts of equation are set:m = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{8 - 2}{13 - 1} = \frac{6}{12} = \frac{1}{2}

To show you in practice that such slope is not very big, watch the gif below.

Slope is used often in everyday life for the steepness of road. Often you will see sign as this one in mountains.

This type means that for 100 meters in horizontal direction you will go up by 10 meters.

Next time I will talk about steepness but this time not only on line where the steepness is always the same but also on curve where it changes every moment though derivatives are capable of solving such problems.

Dragallur

PS: all pictures were from wikipedia page so I will not link them one by one.

 

Limits made easy and continuity

Hi,
yesterday I wrote some basics about functions and today I will write about limits again, and when they are defined and when they are not.

Just to remind you, we will use limits on functions. Those functions will usually be plotted on graph so it is easier to work with them. Our first function we work with will be the one below:

Some function.

If you have not seen that yet, filled dot means that the point is inside of the function and circle means that the point is not there. Now when we speak of limit and if it is defined we have to get the same results as we approach from both sides.

What do I mean by this? Limit is basicly just approaching some number very very close. Take for example x=1. At that point in the function above, y equals 5. If we wanted to take the limit it would go as follow:  

limx→1   f(x)                           [1]

Now if we think about it before we get the result, we know that you can approach one thing in 1st dimension in two directions. Those are in limits noted as from the negative side (-) and positive side (+).

For the limit I wrote, (limx→1   f(x)) from both sides we will get the normal result as if we wanted to know what the function outputs but sometimes we just can not use the limit because  it does not exist.

Such an example would be for the following limit (still working with the first function):

limx→2   f(x)

In this limit we are trying to approach the number two but from the graph we can see that it is strange at that point. The function jumps so we should check the limit from both sides.

limx→2+   f(x) = 1
limx→2–   f(x) = 2

Since the limits do not equal each other, the one before does not exist! We can have so called “one-sided limits” but they are not of much use as far as I know. Now we can actually create amazing definition for continous function!

Continous function is such that does not have any jumps or spaces in it.

example of a discontinuous function with a hole

 

 

The function on the left is discontinous. This is because on one point there is space, which means that function is not defined there.. this is problem if you want to be continous.

 

 

example of a discontinuous function with limits from left and right not equal.

 

Another function is discontinous even that it is defined on all Xs. The problem lies in what I told you about, if we took the limitx→3 f(x) = undefined
This is because from positive and negative side we will get different result.

 

example of a discontinuous function where f(a) and lim f(x) as x approaches a not equal

Again the function is not continous. This time the  limit at 2 exists but it does not equal the value of the function.

limitx→2 f(x) ≠ f(2)

 

 

example of discontinuous function where the limit does not exist, vertical asymptote.

 

 

This one on is not continous either. This is because if we approach from negative values we will get -∞ but if we approach from positive values we will get +∞. The limits do not equal so the function can not be continous.

 

From these points we can summarize what function has to have to be continous at one point.

  1. Point there is defined, it is not empty circle!
  2. Limit on the point exists.
  3. The limit equals to the point on the function.

Or also:

  1. f(a) is defined
  2. limx→ a f(x) exists
  3. limx→ a f(x) = f(a)

This is all from me for now, thanks to “analyzemath.com“. I did not need to create all the graphs again thanks to them.

Dragallur

[1]Sadly wordpress is not able to create some normal indexing so I will write it like this. Normally limit is noted as this:

Proper notation for limit where x approaching something is in the bottom.

Limits made easy and heart equation

Hi,
I said that I started to learn limits. Since often I write about the things I just learn I will start this series today with the very basic. (The start is actually so easy you wont even think that it is precalculus or something)

Basicly the context for limits are functions. I have personally never learned functions on

Basic idea of function

their own and I do plan to do that but I do not think it is so important right now. You just
have to have this idea that when you have function you will give it some input and it will give out some output (kind of black box).
It is important to say that one input corresponds only to one output. You have already probably seen some graphs so it is good to say that you can plot a function.

 

The thing with outputs and inputs can be nicely illustrated on one thing: imagine a class of kids and that you measure them.

Carl – 157 cm
Ann – 152 cm
Caroline – 160 cm
… and so on

Now you will plot them on graph next to each other. In big enough class you would probably have more kids with same height.Limits made easy1

On the left we have three example kids from one class. As is written, Ann has 152 centimeters, Susan 152 too but Jacob has 149,155 and 161 centimeters. Such class would not make a great function! The interesting thing is of course that to one height (152 cm) you can match more people (Ann and Susan), this makes sense. But you can not match one person to more heights! This is the way function works. You could just change names and heights for x and y and you would be there[1]. So if you graph some function it will never be vertical and basicly no two values will ever be above each other, when you on the other hand plot equation you can easily get graph where there are two points above each other:

Heart

Equation stolen from twitter and modified for better look.

So… what role do limits play here? As you probably already heard, limit tolds us what value will function give us when we give it input really close to some number. If you have function like

f(x)=x^2                  (f(x) is the way functions are noted, you could use other symbols)

You can ask for limit of x approaching to any real number and you would get the same as if you would calculate x to the power of 2. The real usage of limits comes when there is point where you can not get some nice value and also I think that it is defined by limits if function is continous (without jumps) or not.

I will slowly continue in the next post 😉

Dragallur

PS: some of my readers mathematicians (or anybody), if there please point out any mistakes, I am just learning this so it would be great to know my mistakes!

[1] To make it even clearer I made this extra picture:

Limits made easy2