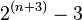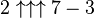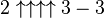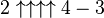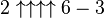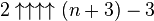On human nature (part 1)

Hi,

Today I was going to write about the book Brave New World and happiness but just few minutes back I settled on something else so I am not even sure what will come out in the next several minutes.

As I was going through my news feed on Facebook I noticed Phil Plait posting again. It is about another black hole merger and gravitational wave detection. This happened I think four or five times now and of course for the first time it was all over the news, everybody was talking about it (even Czech news mentioned it). I am not sure how it was like for the next time but it probably did not get such an attention… now I am not trying to say that it should have, there are other important things (like a woman under root (don’t even ask for the context)). Anyway, this time gravitational wave was detected and public could only find out through reading one tweet ^[1]! That is how much coverage you get for discovery in probably completely new field of physics.

I am certainly quite biased here but the point that Phil Plait made in his post and that I want to share here is how people look for new things but then quickly forget about them. It appears we live in an age where meme (meaning not only joke now) lasts for shorter and shorter time ^[2]. This might be caused by this “information age” or whatever we call the 21^st century but I think this trend also propagates further to the need to have a new iPhone or whatever is behind schedule on being “updated”.

Maybe all of this sounds cliché and just the other day I was telling one of my teachers that the reason why man do not work with hands so much is simply because we live in different time! It reminds me of people worrying about first books then newspapers, TVs and now phones and their effect on youth (this and this XKCD will help you get the idea). And yet should we be worried about the change? How are we going to get ready for it if we leave it to itself and then it does become a problem? I could write under this picture of Black Friday: “Look at those insane people!” but maybe as things tend to be it is more complicated than that (but yeah they are probably buying useless stuff 😀 ).

“Look at them! Sheeple!”

Dragallur

^[1]Yup that is a lie, of course it spread through the internet but it was not such a boom.

^[2]I should probably put disclaimers all over the place since I have not lived very long time yet.

Book review 12) Thing Explainer

Hi,

Cover of the book Thing Explainer

Randall Munroe is a great guy. Creator of XKCD (totally free nerd comics) and the author of What If which you can also read on the internet maybe only some parts… Now one day about two weeks ago I noticed in our school library that they bought his “new” book Thing Explainer. I wanted to buy it earlier but I found out that it costs like almost two new books and was quite discouraged (and I did not have the money anyway). So for some reason the people in the library bought it and I have read it in few days.

Book: Thing Explainer

Author: Randall Munroe

Genre: Science

Pages: dunno

Rating: 10/10

Thing Explainer is a book that explaines complicated stuff in simple words, simple means ten hundred most used words. Great idea I admit. Randall says that when he was younger he purposefully used complicated words so that nobody thought about him, that he did not know them, but in this book he does not need to care about it.

Inside you can find explanations of: Saturn V (Up Goer Five), Keyhole (Shape Checker), Periodic table, Sun, Washing maschine, Car and many many more. There are I think two or three double pages which extend the books already giantic size to double and the page about Skyscraper (Sky toucher) is of the format A2

1000 words is not much. Most technical terms do not exist and even if you know them IRL (in real life) you may find yourself wondering what some things mean. “Fire water” took me some time indeed. Or helium is “kind of air that makes your voice funny”.

Basically there is no objection from me, hopefully the author will write 2nd part since there is lot of stuff outhere that still needs to be covered!

Here is in the same style Einstein and Theory of Relativit explained.
Here is Up Goer Five.

This video is from Minute Physics about getting to space:

Dragallur

XKCD

Hi,
again, it is kind of late so today I will only share with you some cool XKCD pictures and next post will probably be about our asteroid exploration which has 2 major news.

Not the best one but surely up-to-date.

Yeah cameras are great 😉

Pyramid Honey

Thats how conspiracy is created.

To everyone who responds to everything by saying they've 'lost their faith in humanity': Thanks--I'll let humanity know. I'm sure they'll be crushed.

Dragallur

All comics are from XKCD site, thanks Randall

Smiley Thumb Award

Hi,
when I get one of those awards I always wonder who are those people that make these awards! I mean, this must be some special group or what? Maybe I could one day create my own award

hell no.

Anyway I was nominated in the first round of this award because Chape created this brand new award, thanks man for nominating me. So here it is.

The rules:

1. Show your new cool award.

2. Thank whoever nominated you and provide a link to their blog.

3. Tell us what makes you smile.

XKCD makes me smile

4. Select other blogs you want to give the award to. How many is up to you.

I will nominate three which I have never nominated before:

5. Copy and paste the rules.

Thats done.

Dragallur

One week of mathematics, #5

Hi,
this is the last day of one week of mathematics. The last one was not about mathematics much because we were leaving about 13:30.

At the morning we were packing some things and we had only one and last lecture. When I saw the guy who was going to present it I was terrified, when I saw that he takes the same presentation again I was terrified even more. He was saying exactly the same stuff as day before, it was about matrices as I said in last post. Half of the people did not heard it but for the rest it was not useful as last time. Whole time I was reading some posts from you guys and also reading some XKCD. Here are the best, all content is from XKCD site and all credit belongs to the creator, Randall Munroe (he has it under 2.5 CC): einstein[1] advent[1] five_day_forecast[1]

fixion[1]

Oh, I really love those! Anyway, after lunch we drove home. That is all for one week of mathematics, hope you enjoyed.

Dragallur

Turn your brain into supermassive black hole

Hi,
here it comes here it goes! Today I am writing probably the last post from Brazil since I am leaving in Tuesday. Maybe tommorow after seeing Christ in Rio, I will be able to write another one.
Anyway, here comes the promised post about Ackermann function.

Ackermann function is a function with two inputs and it is growing extremely fast. To see the results it is best to make a table. Ackermann
function is written like this: A(m,n).
There are few types of Ackermann function because some people made their modifications of it to fit their plans. Here I will mention the most famous one.
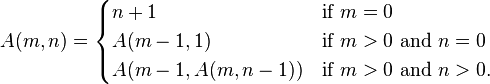$A(m, n) = \begin{cases} n+1 & \mbox{if } m = 0 \\ A(m-1, 1) & \mbox{if } m > 0 \mbox{ and } n = 0 \\ A(m-1, A(m, n-1)) & \mbox{if } m > 0 \mbox{ and } n > 0. \end{cases}$ So lets see what this function means:
A(m,n) is the input of this. If m=0 then you will make n+1 and find it in the table which is below.
If m is bigger than 0 and n=0 then you will call Ackermann function again with m-1 and n=1.
Last one, when you have m>0 and n>0 then you call the function again with m lowered by one and n will be defined by another A function which obeys

m\n	0	1	2	3	4	n
0	1	2	3	4	5	$n + 1$

the rules again. Lets see the table. This is the first row which is extremely simple. M is the vertical axis. So when the arguments are A(0,0) then you go as follows: m=0 which means that you higher n by one which is 1 and that is the result.

If A(3,2) it gets very messy: here you go.
A(3,2)
A(2,A(3,1) — because n and m are higher than 0 you lower m by one and then you call another function with n lowed by one.
A(2,A(2,A(3,0) — both are still higher, so you do the same thing again..
A(2,A(2,A(2,1) — change the function from A(3,0) to A(2,1) because n is 0 according to rule above
A(2,A(2,A(1,A(2,0)
A(2,A(2,A(1,A(1,1)
A(2,A(2,A(1,A(0,A(1,0)
A(2,A(2,A(1,A(0,A(0,1)
A(2,A(2,A(1,A(0,2)
A(2,A(2,A(1,3)
A(2,A(2,A(0,A(1,2)
A(2,A(2,A(0,A(0,A(1,1)
A(2,A(2,A(0,A(0,A(0,A(1,0)
A(2,A(2,A(0,A(0,A(0,A(0,1)
A(2,A(2,A(0,A(0,A(0,2)
A(2,A(2,A(0,A(0,3)
A(2,A(2,A(0,4)
A(2,13) — I skipped lot of the steps because it is such a mess when you have to do it whole again but it equals 29.
=29

Values of A(m, n)
m\n	0	1	2	3	4	n
0	1	2	3	4	5	$n + 1$
1	2	3	4	5	6	$n + 2 = 2 + (n + 3) - 3$
2	3	5	7	9	11	$2n + 3 = 2\cdot(n + 3) - 3$
3	5	13	29	61	125	$2^{(n + 3)} - 3$
4	13 = ${2^{2^{2}}}-3$	65533 = ${2^{2^{2^{2}}}}-3$	2⁶⁵⁵³⁶ − 3 = ${2^{2^{2^{2^{2}}}}}-3$	${2^{2^{65536}}} - 3$ = ${2^{2^{2^{2^{2^{2}}}}}}-3$	${2^{2^{2^{65536}}}} - 3$ = ${2^{2^{2^{2^{2^{2^{2}}}}}}}-3$	$\begin{matrix}\underbrace{{2^2}^{{\cdot}^{{\cdot}^{{\cdot}^2}}}} - 3\\n+3\end{matrix}$
5	65533 = $2\uparrow\uparrow\uparrow 3 - 3$	$2\uparrow\uparrow\uparrow 4 - 3$	$2\uparrow\uparrow\uparrow 5 - 3$	$2\uparrow\uparrow\uparrow 6 - 3$	$2\uparrow\uparrow\uparrow 7 - 3$	$2\uparrow\uparrow\uparrow (n+3) - 3$
6	$2\uparrow\uparrow\uparrow\uparrow 3 - 3$	$2\uparrow\uparrow\uparrow\uparrow 4 - 3$	$2\uparrow\uparrow\uparrow\uparrow 5 - 3$	$2\uparrow\uparrow\uparrow\uparrow 6 - 3$	$2\uparrow\uparrow\uparrow\uparrow 7 - 3$	$2\uparrow\uparrow\uparrow\uparrow (n+3) - 3$

Here is the rest of the start of the table. It increases rapidly since it repeats over and over again (this is called recursion). You see that you have to use Knuth`s up-arrow notation.
Now you see why A(G64,G64) is such spawn of hell.
The reason for Ackermann function to exist and to be so famous is that it is one of the first functions that are used in computability theory. It is the theory which asks what means that the function is not computable and how much not computable it is. Computable functions are those for which we can find some algorithms, and algorithms are very important. For example in computations.
It seems for example that there is no computable function for finding prime numbers or at least no efficient one.

Dragallur

M	T	W	T	F	S	S
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

Science and rationality

Universe and everything

xkcd

On human nature (part 1)