Hi,
here it comes here it goes! Today I am writing probably the last post from Brazil since I am leaving in Tuesday. Maybe tommorow after seeing Christ in Rio, I will be able to write another one.
Anyway, here comes the promised post about Ackermann function.
Ackermann function is a function with two inputs and it is growing extremely fast. To see the results it is best to make a table. Ackermann
function is written like this: A(m,n).
There are few types of Ackermann function because some people made their modifications of it to fit their plans. Here I will mention the most famous one.
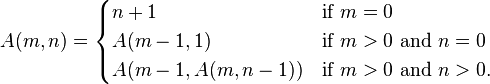 So lets see what this function means:
So lets see what this function means:
A(m,n) is the input of this. If m=0 then you will make n+1 and find it in the table which is below.
If m is bigger than 0 and n=0 then you will call Ackermann function again with m-1 and n=1.
Last one, when you have m>0 and n>0 then you call the function again with m lowered by one and n will be defined by another A function which obeys
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |  |
the rules again. Lets see the table. This is the first row which is extremely simple. M is the vertical axis. So when the arguments are A(0,0) then you go as follows: m=0 which means that you higher n by one which is 1 and that is the result.
If A(3,2) it gets very messy: here you go.
A(3,2)
A(2,A(3,1) — because n and m are higher than 0 you lower m by one and then you call another function with n lowed by one.
A(2,A(2,A(3,0) — both are still higher, so you do the same thing again..
A(2,A(2,A(2,1) — change the function from A(3,0) to A(2,1) because n is 0 according to rule above
A(2,A(2,A(1,A(2,0)
A(2,A(2,A(1,A(1,1)
A(2,A(2,A(1,A(0,A(1,0)
A(2,A(2,A(1,A(0,A(0,1)
A(2,A(2,A(1,A(0,2)
A(2,A(2,A(1,3)
A(2,A(2,A(0,A(1,2)
A(2,A(2,A(0,A(0,A(1,1)
A(2,A(2,A(0,A(0,A(0,A(1,0)
A(2,A(2,A(0,A(0,A(0,A(0,1)
A(2,A(2,A(0,A(0,A(0,2)
A(2,A(2,A(0,A(0,3)
A(2,A(2,A(0,4)
A(2,13) — I skipped lot of the steps because it is such a mess when you have to do it whole again but it equals 29.
=29
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |  |
| 1 | 2 | 3 | 4 | 5 | 6 |  |
| 2 | 3 | 5 | 7 | 9 | 11 |  |
| 3 | 5 | 13 | 29 | 61 | 125 | 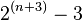 |
| 4 | 13
= |
65533
= |
265536 − 3
= |

= |

= |
 |
| 5 | 65533
= |
 |
 |
 |
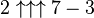 |
 |
| 6 | 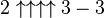 |
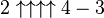 |
 |
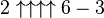 |
 |
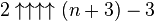 |
Here is the rest of the start of the table. It increases rapidly since it repeats over and over again (this is called recursion). You see that you have to use Knuth`s up-arrow notation.
Now you see why A(G64,G64) is such spawn of hell.
The reason for Ackermann function to exist and to be so famous is that it is one of the first functions that are used in computability theory. It is the theory which asks what means that the function is not computable and how much not computable it is. Computable functions are those for which we can find some algorithms, and algorithms are very important. For example in computations.
It seems for example that there is no computable function for finding prime numbers or at least no efficient one.
Dragallur







